Auteur: Chérif F. Matta
Département de chimie et physique, Université Mont-Saint-Vincent, Halifax, Nouvelle-Écosse, Canada
Département de chimie, Université Laval, Québec, Québec, Canada
cherif.matta@msvu.ca
Résumé
Les réseaux sont partout : les neurones dans le cerveau, les rues ou la grille électrique d’une ville, les motifs d’amitié sur les réseaux sociaux, les atomes dans une molécule, etc. Tous forment des réseaux. Il est intéressant de noter que toutes ces réalisations physiques très différentes des réseaux peuvent être traitées par des techniques de la théorie des graphes, ce qui leur confère une sorte de coïncidence mathématique. Un réseau peut être représenté par un graphe qui, à son tour, peut être représenté par une matrice de connectivité. L’étiquetage des sommets d’un graphe et de sa représentation matricielle étant arbitraire nous devons extraire des propriétés qui n’en dépendent pas, c’est-à-dire des « invariants de matriciels ». Ces techniques s’avèrent précieuses pour développer des modèles prédictifs en chimie à partir des invariants de ce que l’on appelle « les matrices de localisation et de délocalisation d’électrons » (abrégé en anglais comme LDMs). En croisant les disciplines, cette approche est une incarnation de la transdisciplinarité telle qu’envisagée par ses fondateurs Basarab Nicolescu et Edgar Morin.
Mots-clés : Connectivité, topologie, théorie des graphes chimiques, chimie quantique, réseaux atomiques dans une molécule, matrices de localisation et de délocalisation d’électrons (LDMs).
- L’omniprésence des réseaux et leurs graphes topologiques correspondants
Par « réseau », nous entendons un système composé de « nœuds » (ou « sommets ») reliés par des « arêtes » (liens) entre eux. Ni la nature physique des nœuds ni celle des arêtes n’ont d’importance pour définir la topologie (la connectivité) d’un réseau donné. C’est seulement la connectivité qui compte. Le plan du métro d’une grande ville est un exemple pertinent d’un graphe représentant un réseau. Dans ce cas, seule la connectivité des lignes du métro compte pour déterminer le chemin optimal d’une destination à une autre. Le plan est également efficace même si les distances entre les stations (les nœuds) sont déformées, hors de proportion, par rapport aux distances réelles entre les stations car cela ne change en rien les étapes qui déterminent le chemin du parcours. Ce dernier ne dépend que de la connectivité, autrement dit, de sa topologie.
Dans un article, Michael Polanyi écrit : « La physique est muette sans le don des conditions limites, qui forment son cadre ; et ce cadre n’est pas déterminé par les lois de la physique[1]» (Polanyi, 1967) ; il continue dans un autre article : « Nous avons vu que la physiologie interprète l’organisme comme un réseau complexe[2] de mécanismes, et qu’un organisme est comme une machine, un système sous double contrôle. Sa structure est celle d’une condition aux limites mettant les substances physico-chimiques de l’organisme au service de fonctions physiologiques[3] » (Polanyi, 1968).
Comme l’explique Polanyi, même si les propriétés d’un réseau complexe ne sont pas au-delà des lois physiques, ces propriétés ne peuvent pas être réduites à ces lois. Elles sont de vraies propriétés émergentes pour ainsi dire. Un réseau est donc doté de propriétés émergentes qui sont intimement associées à la seule connectivité du réseau. Si on change cette connectivité entre les nœuds du réseau (sa topologie) ses propriétés émergentes changent en conséquence.
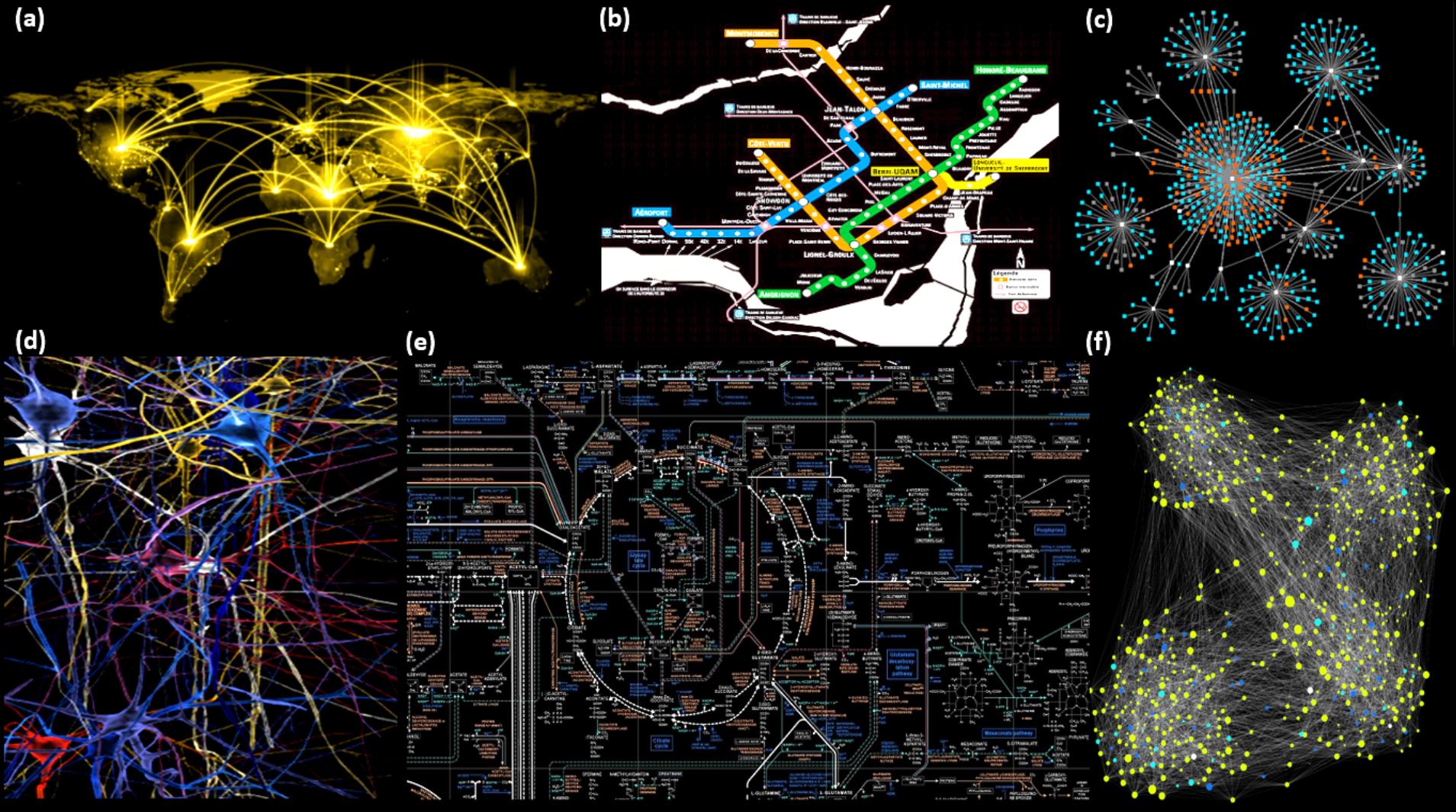
Les réseaux sont partout (voir Figure 1). On les rencontre dans la manière dont les neurones du tissu cérébral sont connectés, dans les réseaux sociaux tels que Facebook, dans les sciences du comportement, par exemple, les patrons de citation dans la littérature, dans les réseaux neuronaux qui sont à la base des algorithmes d’intelligence artificielle, dans l’interconnectivité et interdépendance des réactions biochimiques, dans le réseau électrique d’une ville, dans le réseau d’approvisionnement en aliments ou en eau, dans les réactions atmosphériques, dans la propagation de maladies durant les pandémies (par exemple), dans les connections des routes et moyeux centraux (hubs) aériens ou maritimes à travers le monde, etc. (Aldous and Wilson, 2000; Huang and Parker, 1971; Slepian, 1968; Solé, 2009; Sporns, 2018; van Dixhoorn and Evans, 1974). Un réseau qui s’autoajuste par boucles de rétroaction constitue un système complexe comme le définit von Bertalanffy (1969). Une molécule peut aussi être considérée comme un réseau de liaisons chimiques (arêtes) liants des nœuds (atomes), un approche qui forme la base de toute la théorie chimique des graphes (Aldous and Wilson, 2000; Balaban, 1976; Balaban, 1985; Balasubramanian, 1994; Bonchev and Rouvray, 1991; Diudea et al., 1999; Dmitriev, 1981; Janezic et al., 2007; Matta, 2018; Toussi et al., 2020; Wawer et al., 2008).
Figure 1: L’omniprésence des graphes : (a) Les principales lignes d’aviation reliant le globe, (b) le plan du métro d’une métropole, (c) les connections des « amis » d’un réseau sociale comme Facebook, (d) les neurones du cerveau, (e) les réactions biochimiques dans une cellule vivante, (f) les points de contacts entre personnes dans un modèle de la propagation d’une épidémie.
Les mêmes techniques mathématiques sont utilisées pour tirer d’un graphe les propriétés qui ne dépendent que de sa topologie. Une première étape dans cette direction serait de représenter le graphe par une matrice de connectivité. Mais il y a un problème, la matrice de connectivité n’est pas unique car elle dépend de l’étiquetage des nœuds. Quoi faire pour surmonter cet obstacle ? C’est un problème qui a été résolu par les mathématiciens, il y a très longtemps : il s’agit d’extraire des matrices de connectivité des « invariants mathématiques », c’est-à-dire des objets mathématiques qui sont uniquement dépendants de la topologie et non pas de l’étiquetage qui est nécessairement arbitraire. Essentiellement ces mêmes techniques mathématiques sont utilisées pour extraire les invariants de n’importe quelle matrice de connectivité qui décrit n’importe quel réseau que ce soit celui de neurones dans le cerveau, celui du métro d’une grande métropole, ou celui des liaisons chimiques liants les atomes d’une molécule donnée.
Cette omniprésence des graphes dans des domaines tant variés comme nous venons de le souligner fait de leur étude un projet nécessairement transdisciplinaire. Bien que dans un contexte différent, Basarab Nicolescu écrit en 1996 dans La Transdisciplinarité – Manifeste que « [c]es différentes entités vivaient dans leur propre monde, régi par ses propres lois, mais elles étaient reliées par des lois cosmiques communes engendrant un ordre cosmique commun » (Nicolescu, 1996). Cet « ordre cosmique commun » engendré par les représentations matricielles des différents réseaux est la manière unifiée d’un extraire des invariants qui ne dépendent pas de l’étiquetage. En complet accord avec cette définition de Nicolescu, Edgar Morin propose, en 1990, la définition suivante de la transdisciplinarité : « En ce qui concerne la transdisciplinarité, il s’agit souvent de schèmes cognitifs qui peuvent traverser les disciplines, parfois avec une virulence telle qu’elle les met en transes[4]» (Morin, 1990). Cette dernière définition nous servira de guide dans cet exposé où son application à la théorie des graphes sera brièvement explorée.
- La représentation matricielle du graphe d’un réseaux
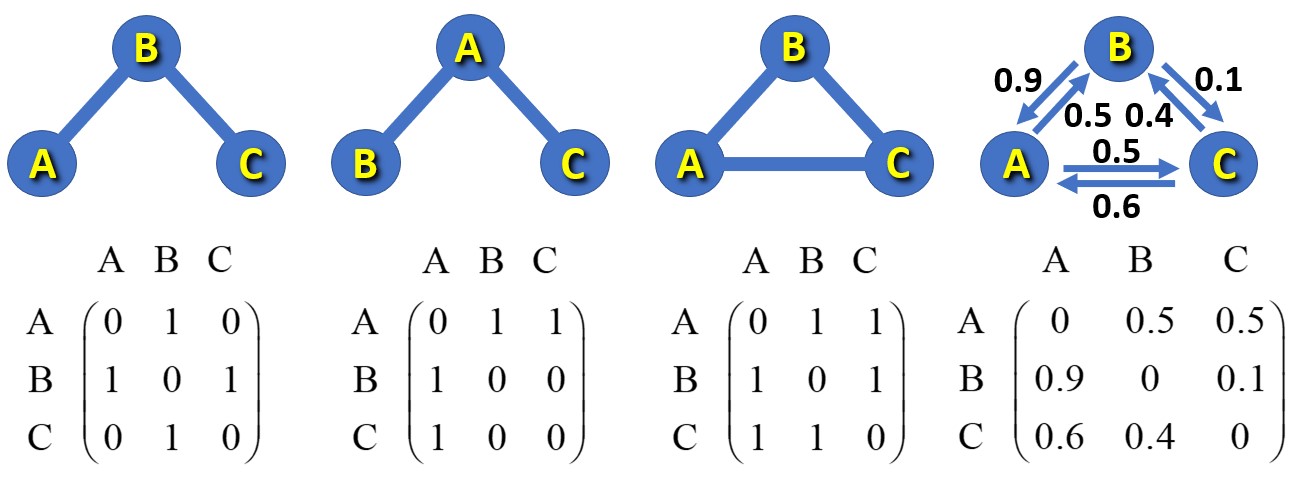
En guise d’exemple, la Figure 2 représente la connectivité de réseaux de trois nœuds. Les trois premiers réseaux (de gauche à droite) sont représentés par des « graphes non-orientés » où les arêtes sont liées par des liaisons symétriques (qui ne dépendent pas de la direction p. ex. AB = BA, etc.) En revanche, les arêtes du graphe de droite sont non-symétriques avec différentes probabilités en allant de A ver B que de B vers A, etc. Ce dernier est un exemple d’un « graphe orienté ». Au bas de la figure, pour chaque graphe est donnée une représentation matricielle possible (remarquons que celle-là n’est pas unique car on peut permuter l’ordre des lignes et des colonnes en obtenant une autre matrice qui est également valable comme représentante du même graphe). En outre, remarquons que si l’on change l’étiquetage des arêtes en allant de la première représentation de gauche de la figure à la suivante, la matrice change en conséquence.
Puisque les propriétés physiques ne peuvent pas dépendre de cet étiquetage arbitraire, seules les propriétés des matrices qui sont indépendantes de l’étiquetage – les invariants matricielles – ont une signification physique. On tire, par exemple, des deux matrices de gauche (de la Figure 2) le même polynôme caractéristique (2l-l3), les mêmes valeurs propres (l1,2 = ±2½, l3 = 0), les mêmes vecteurs propres, etc.
Figure 2 : Panneau du haut (de gauche à droite) : un graphe non-orienté de trois nœuds et deux arêtes, le même graphe qui décrit le même réseau et la même topologie mais après un changement d’étiquetage, un autre graphe non-orienté qui consiste de trois nœuds et de trois arêtes, le même graphe mais orienté avec différentes probabilités de transition d’un nœud au suivant. Panneau du bas : représentation des graphes correspondants.
- Les réseaux et leurs graphes topologiques comme « schèmes cognitifs » qui peuvent traverser les disciplines
Il serait avantageux d’illustrer le concept de « schème cognitif » quant à la représentation matricielle de réseaux appartenant à des domaines très différents par deux exemples concrets (choisis de milliers d’autres exemples qui remplissent la littérature). Ici nous nous focaliserons sur les matrices représentantes des chaînes dites de Markov. Une chaîne de Markov est un processus doté d’une mémoire de l’état (ou des états) précédent(s) du système. Une chaîne d’ordre zéro est un processus dépourvu de mémoire (la probabilité de l’état actuel est indépendante des états précédents). Une chaîne de premier ordre est une dont la probabilité de l’état actuelle dépend seulement de l’état précédant. Les chaînes d’ordres supérieurs dépendent des états de plus en plus antérieurs.
3.1. Chaînes de Markov : un exemple des sciences économiques
Pour simplifier l’exposition, définissons l’état (1) comme celui d’un marché haussier, c’est-à-dire une période de hausse générale des prix, l’état (2) comme un marché baissier, c’est-à-dire une période de baisse générale du marché boursier, et l’état (3) comme un marché stagnant, définit comme une période d’immobilité économique.
Supposons qu’une étude historique sur une période suffisamment longue a révélé les relations probabilistes données par le graphe topologique de la Figure 3. Le graphe donne les diverses probabilités d’avoir un marché d’un type donné, durant une tranche de temps (disons cinq années) étant donné la nature du marché dans la tranche précédente. Par exemple, de la figure 3, la probabilité d’un marché haussier dominant la tranche de temps suivante à un marché stagnant est de 0.25, mais celle d’un marché stagnant suivant un marché haussier est dix fois plus petite (de seulement 0.025). Cependant la probabilité d’une période de marché haussier suivant une autre de marché haussier est d’une probabilité de 0.9.
Figure 3: Un graphe orienté et une de ces représentations matricielles montrant les relations probabilistes entre un état économique et l’état qui le précède immédiatement (une chaîne de Markov de premier degré) qui consiste de trois nœuds et neuf arêtes dirigées.
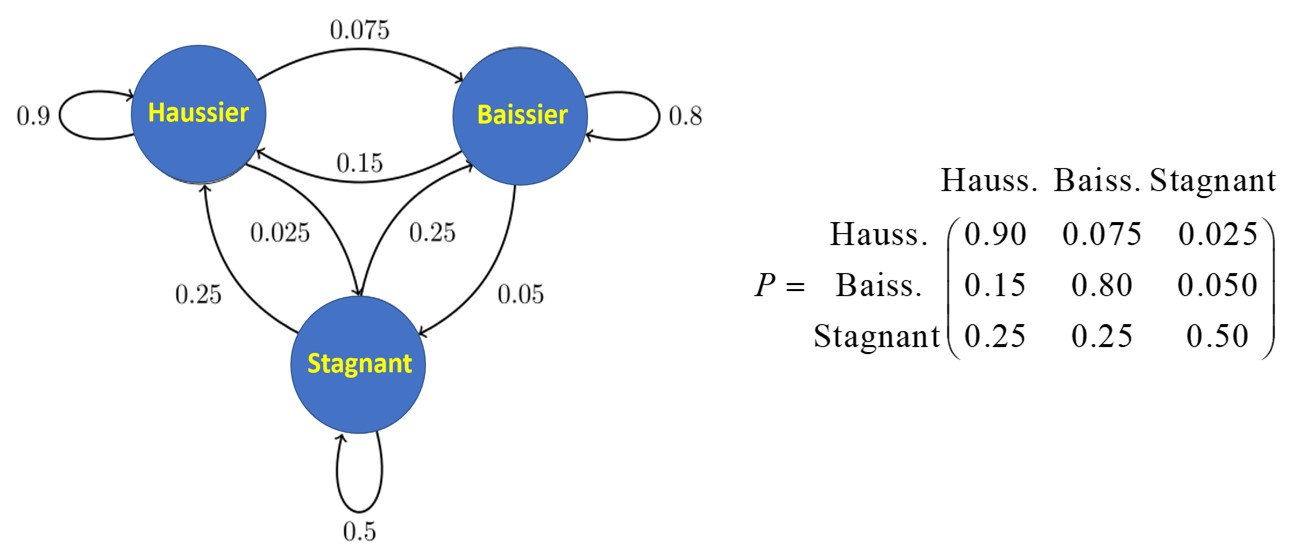
Soit, on est face à un « vecteur d’état », c’est-à-dire un vecteur de dimension 3, puisqu’il existe trois états économiques dans ce modèle [haussier, baissier, stagnant]. On place « 1 » dans la case échéante et zéro dans les deux autres. Donc, le vecteur d’état d’un marché baissier serait [0,1,0], etc. La question maintenant est : comment prédire un état dans, disons 3 étapes temporelles, c’est-à-dire dans la tranche de temps de 15 à 20 ans dès la fin de la période présente ? Est bien c’est simplement un produit matriciel du vecteur d’état présent multiplié par le cube de la matrice de probabilité P.
Cela donne : [0,1,0] P3 = [0.36, 0.57, 0.07].
Autrement dit, cela signifie qu’étant donné une période de marche baissier, trois périodes (15 ans) plus tard, il y a 36 % de probabilité d’avoir un marché haussier, 57 % d’avoir un marché baissier, et seulement 7 % de chances d’avoir un marché stagnant.
3.2. Chaînes de Markov : un exemple de la biologie moléculaire
La séquence des bases d’une molécule d’ADN (ou d’ARN) peut être approximativement décrite comme une chaîne de Markov du premier degré où la probabilité d’apparition d’une base particulière des quatre (adénine-A, thymine-T, guanine-G, et cytosine-C) ne dépend statistiquement que de la base qui la précède immédiatement dans la séquence. Cela peut être représenté par le réseau de la Figure 4 dans lequel les probabilités sont fictives pour le seul but de l’illustration.
Dans ce cas, le vecteur d’état est de dimension 4, [A, T, G, C]. Soi une sequence d’ADN [… A A A T G C G C A x1 x2 x3 x4 x5 x6 x7 x8 X …], ou les huit x sont des bases non-spécifiées. Dans ce cas, quelles sont les probabilités des quatre bases à la 9ème position X ? Pour cela il suffit de multiplier le vecteur représentant la dernière base connue (la base A), c’est-à-dire le vecteur B = [1, 0, 0, 0], par la matrice de transition à la puissance 8.
Figure 4: Un graphe orienté et l’une de ces représentations matricielles illustrant les relations probabilistes entre une base d’ADN et la base qui la précède immédiatement dans la séquence (une chaîne de Markov de premier degré).
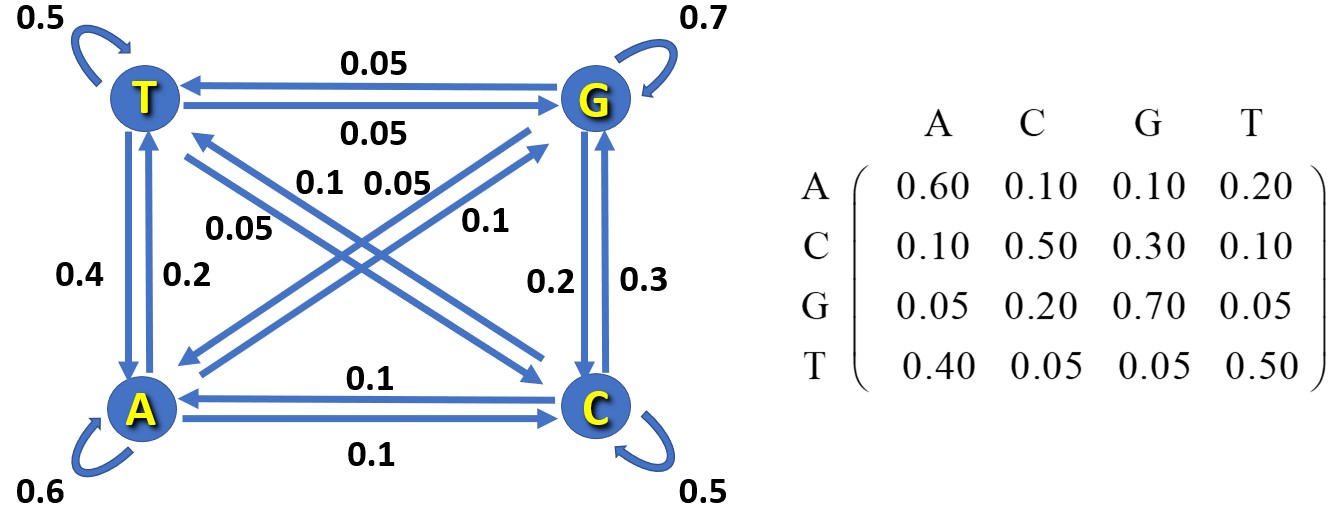
Explicitement, en utilisant la matrice de la Figure 4, nous aurons :
Figure 5 : Développement de la Figure 4.
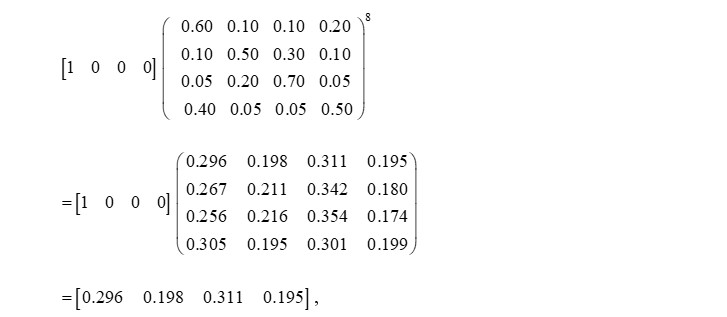
Ce qui a comme conséquence que la base la plus probable huit places en avant d’une base A est la G avec une probabilité de 31.1 % suivie de A elle-même avec une probabilité de 29.6 % etc.
- L’extension du concept de réseau et de graphe topologique aux molécules[5]
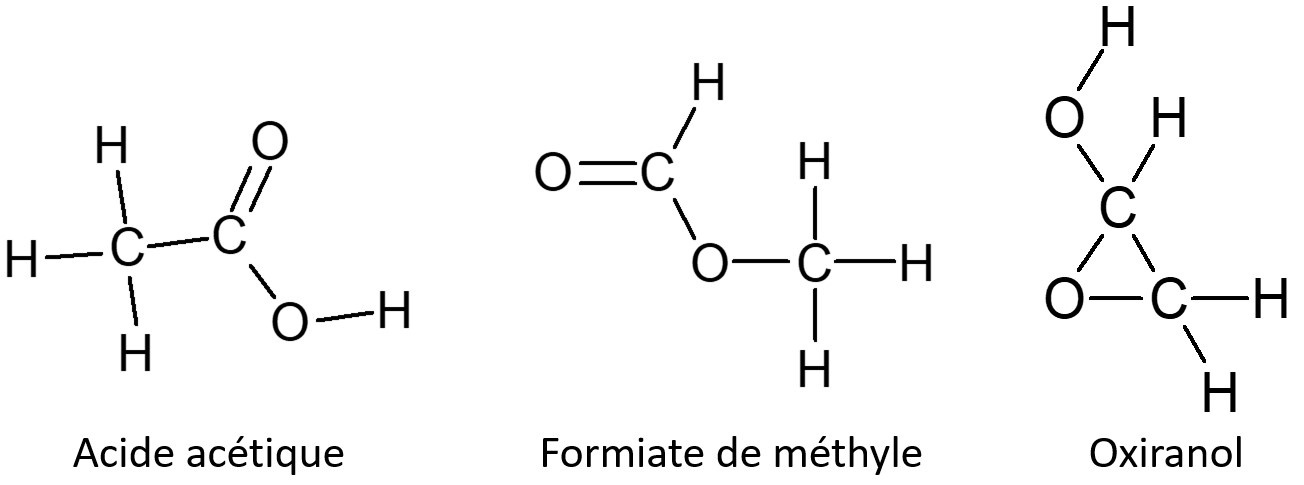
La loi des proportions multiples de John Dalton de 1803 marque les débuts de la théorie atomique moderne de la matière, tandis qu’Avogadro a introduit en 1811 l’idée de la molécule comme un composite d’« atomes dans des molécules » qui se comportent collectivement comme l’unité fondamentale d’un composé chimique donné. Durant la seconde moitié du XIXe siècle, plusieurs savants comme Kekulé, Couper, Loschmidt parmi d’autres ont commencé ce qui est devenu une tradition consistant à dessiner les « structures chimiques » en reliant les symboles atomiques par des lignes introduisant ainsi les premiers « graphes chimiques », quotidiennement utilisés comme outil de prévision de la réactivité et des propriétés chimiques. C’est bien la topologie d’un ensemble donné d’atomes en interaction, un composé chimique, qui fait toute la différence entre, disons, l’acide acétique (le constituant acide du vinaigre), l’oxiranol (un intermédiaire dans la chimie interstellaire et un précurseur de l’oxyde d’éthylène utilisé comme désinfectant) et le réfrigérant toxique formiate de méthyle ! Tous les trois sont composés de deux atomes de carbone, quatre atomes d’hydrogène et deux atomes d’oxygène, mais quelle différence la topologie peut faire ! (Figure 6).
Figure 6: Structures chimiques de trois isomères partageants la même formule moléculaire (C2O2H4) mais qui diffèrent en topologie : Le composant acide du vinaigre (acide acétique), un intermédiaire industriel, insecticide, et réfrigérant (formiate de méthyle), et enfin une molécule qui est le précurseur possible du glycolaldéhyde dans l’espace interstellaire et un précurseur de l’oxyde d’éthylène utilisé comme désinfectant dans les hôpitaux (oxiranol).
Plus tard, au début du XXe siècle, Gilbert Newton Lewis a introduit le concept de pair d’électrons comme étant la base de ce qui est la « liaison chimique ». Cependant, jusque dans les années soixante du siècle dernier, personne n’avait jamais vu de ligne reliant des atomes dans l’espace. Cette ligne reliant les atomes dans un espace tridimensionnel réel (le réseau de liaisons reliant les symboles atomiques), est resté un simple résumé abstrait de l’expérience expérimentale jusqu’à ce que Richard F. W. Bader propose une théorie maintenant appelée la « théorie quantique des atomes dans les molécules » (QTAIM, en abrégé anglais) (Bader, 1990; Matta, 2017).
La théorie QTAIM part de la densité électronique des molécules, des complexes et des cristaux et analyse la topographie tridimensionnelle de ce champ scalaire. Ce faisant, Bader a élaboré une théorie de la structure chimique et de sa stabilité structurelle basée, dans certains de ses concepts fondamentaux, sur la « théorie des catastrophes » de René Thom (Thom, 1977).
Bader a découvert ce que l’on appelle le « chemin de liaison », qui est une ligne de densité électronique maximale reliant les noyaux d’atomes connus pour être chimiquement liés. Dans la grande majorité des cas, la topologie des chemins de liaison représente parfaitement la structure déduite de la chimie expérimentale, mais à quelques exceptions près, ces exceptions peuvent figurer parmi les cas les plus intéressants (ceci est hors de notre propos ici).
Le réseau des chemins de liaison fournit une définition rigoureuse et sans ambiguïté d’une structure chimique et des points de catastrophe où il y a un changement de topologie (et donc un changement brusque de structure). (Le mot « structure » (connectivité) est utilisé ici avec précaution et ne doit pas être confondu avec « géométrie » comme on le fait souvent dans la littérature).
Ces idées ont permis le développement de toute une mécanique quantique de systèmes électroniques ouverts, c’est-à-dire d’atomes dans des molécules (Bader, 1990; Matta, 2017). La densité électronique est observable expérimentalement, surtout à partir des années 1980, lorsqu’on assiste à l’événement des détecteurs modernes, des ordinateurs, de toute sorte de dispositifs capables d’atteindre des températures ultra-basses et de sources très intenses de rayons X (comme les synchrotrons) ; l’environnement était destiné à aller au-delà de l’approximation sphérique pour affiner les données expérimentales obtenues de la diffraction des rayons X par le réseau cristallin. Cela a abouti à ce que, désormais, les chemins de liaison soient régulièrement observés expérimentalement – une vraie première qui est restée jusque-là une abstraction.
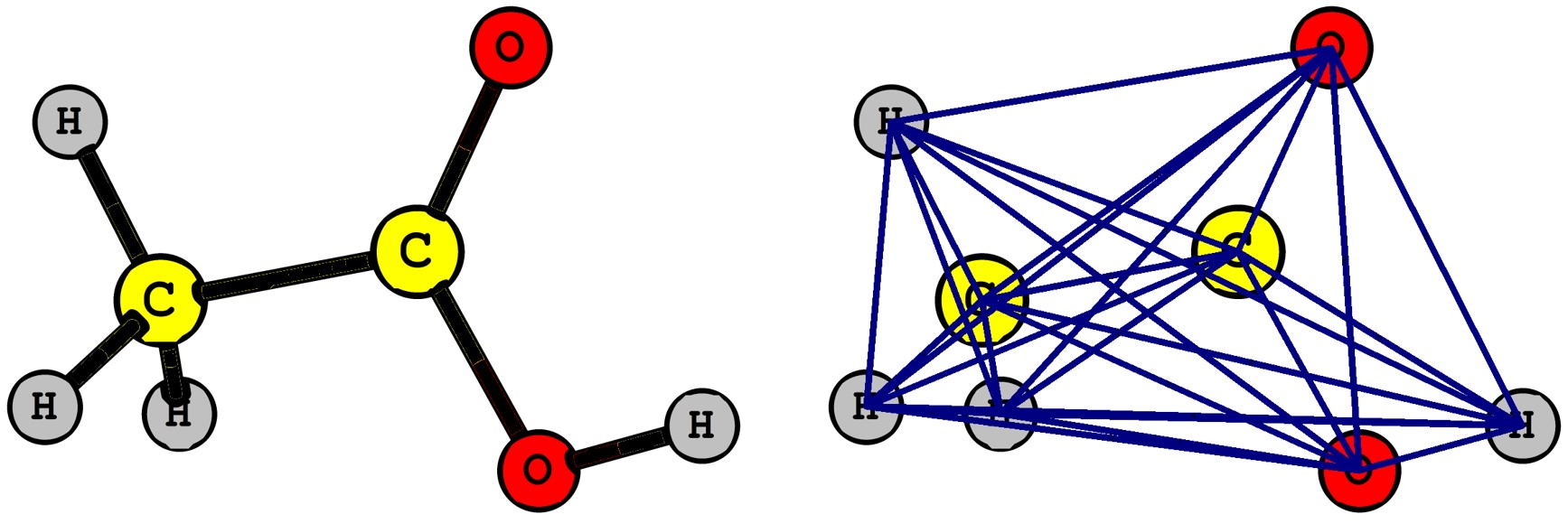
Le graphe moléculaire est en général incomplet. Seulement certaines paires d’atomes sont liées par des liaisons chimiques (et non toutes les paires possibles). Par exemple, la Figure 5 représente des graphes incomplets avec 7 ou 8 liaisons entre 8 atomes (alors qu’un graphe complet devrait en avoir 28 liaisons – voir Figure 7). En se basant sur la théorie QTAIM, nous pouvons aller plus loin en décrivant une molécule par son graphe complet, c’est-à-dire que chaque paire d’atomes est liée par une arête, ici cette arête représente les électrons délocalisés entre ces pairs d’atomes (Cook, 2017; Cook et al., 2023; Matta, 2014; Matta, 2014; Matta, 2018; Sumar et al., 2015; Sumar et al., 2016). Dans la Figure 7 se trouve contrasté un graphe incomplet de la molécule d’acide acétique avec son graphe complet.
Figure 7: Comparaison d’un graphe moléculaire incomplet idéalisé (n = 8 atomes (nœuds), p = 7 (liaisons chimiques (arêtes) avec le graphe complet du réseau formé des chemins d’échange d’électrons (n = 8, p = 28) d’une molécule d’acide acétique.
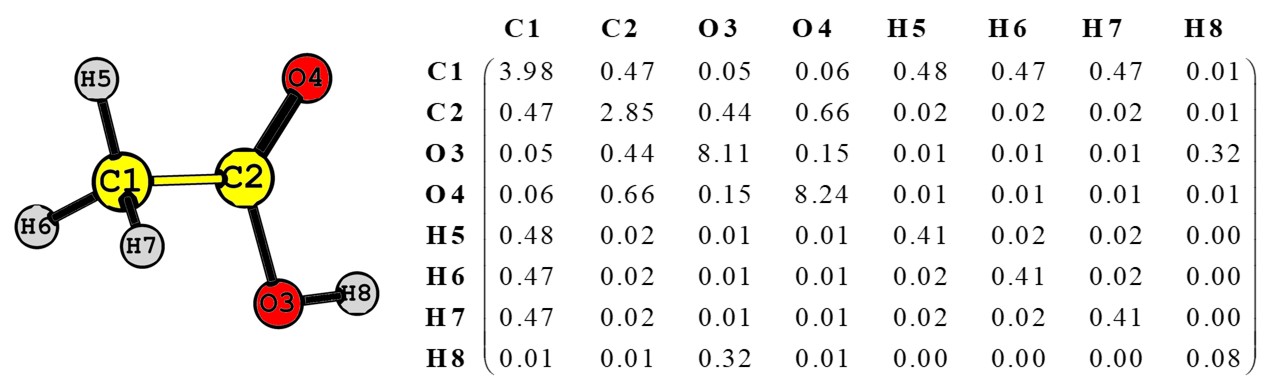
En définissant une matrice de localisation et de délocalisation d’électrons (en abrégé LDM), on peut extraire plusieurs invariants qui peuvent être utilisés pour bâtir des modèles type relations structure-activité quantitatives (QSAR). Un exemple d’une telle matrice LDM est donné dans la Figure 8 pour la molécule d’acide acétique. Les éléments diagonaux de cette matrice représentent le nombre d’électrons localisés dans un certain bassin atomique indiqué par l’étiquette de la colonne ou de la ligne où l’élément se trouve. Chaque élément non-diagonale représente le nombre d’électrons délocalisés entre les deux atomes qui étiquettent la colonne et la ligne de cet élément (divisé par 2).
Figure 8 : Le graphe moléculaire d’une molécule d’acide acétique avec l’étiquetage atomique utilisé pour construire la matrice de localisation et de délocalisation d’électrons (LDM) adjacente. Pour illustrer : l’élément diagonal de la ligne O3 et la colonne O3 indique que 8.11 électrons sont localisés dans le bassin atomique de l’atome d’oxygène numéroté O3 tandis que l’élément non-diagonal de la ligne O4 et de la colonne C2 (ou aussi celui de la ligne C2 et de la colonne O4) signifie que 0.66 x 2 = 1,32 électrons sont délocalisés et également partagés entre l’atome de carbone C2 et l’atome d’oxygène O3. La somme des entrés d’une colonne ou d’une ligne est égale au nombre total d’électons attribué à cet atome (par exemple l’atome C1 contient 3.98+0.47+0.05+0.06+0.48+0.47+0.47+0.01 = 5.99 électrons).
Les invariants des matrices LDM ont été utilisés extensivement pour prédire les propriétés des matériaux, des inhibiteurs d’enzymes, de l’activité ainsi que du mode d’action des répulsifs contre les insectes, de l’activité et du mode d’action des inhibiteurs de corrosion etc. (Cook et al., 2023). Une des méthodes d’extraire des invariants des LDMs est l’analyse en composantes principales (PCA), une approche statistique bien connue qui réduit la dimensionnalité des données et qui est largement utilisée en sciences physiques, sociales et économiques.
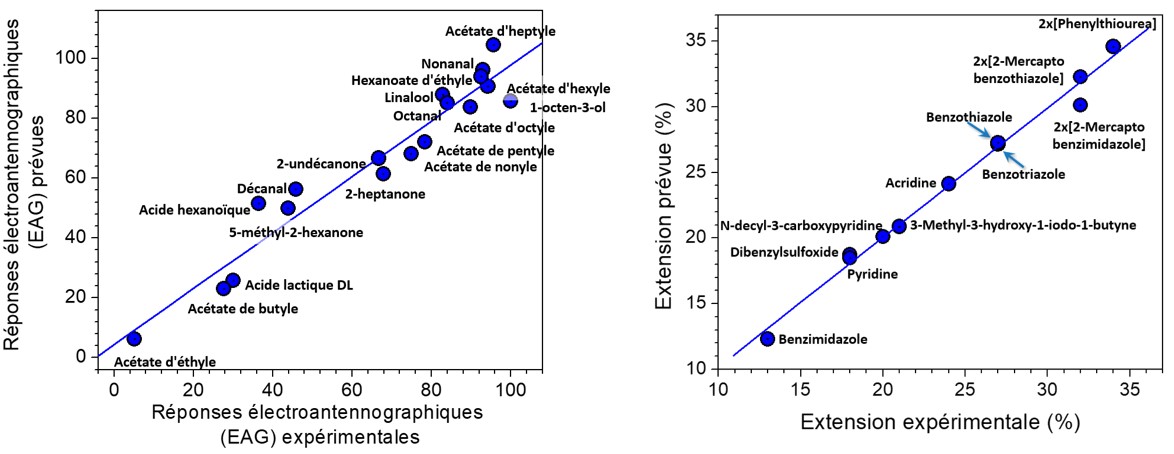
Les composantes principales des LDMs de séries de molécules peuvent être utilisées pour prédire l’activité de molécules qui ne figurent pas dans la base de données. La Figure 9 ne donne que deux exemples où les composantes principales montrent les données expérimentales avec précision. Le tracé à gauche de la figure montre l’excellente corrélation entre la réponse électroantennographique (EAG) de l’antenne du moustique Anopheles funestus, le vecteur principal de la malaria, aux répulsifs contre les insectes couramment utilisés. Quant au tracé de droite, celui-ci démontre l’excellent accord entre l’élongation tolérée (avant la rupture) d’un fil de fer en présence d’inhibiteurs de corrosion communs mesurée expérimentalement et celle prédite en utilisant les composantes principales des LDMs de cette famille de composés chimiques (pour plus de détails techniques et d’exemples, voir Cook et al., 2023).
Figure 9: Deux exemples démontrant le pouvoir prédictif de l’analyse des matrices de localisation et de délocalisation d’électrons (LDMs). À gauche : la relation entre la réponse électroantennographique (EAG) de l’antenne du moustique Anopheles funestus aux répulisfs contre les insectes couramment utilisés. À droite, l’élongation maximale (avant la rupture) d’un fil de fer en présence d’inhibiteurs de corrosion mesurée expérimentalement et celle prédite à partir des LDMs.
5. Remarques finales
La nature transdisciplinaire de l’étude des réseaux provient donc du fait que la théorie mathématique ne dit absolument rien sur la nature des nœuds ou des arêtes. La théorie des graphes fournit le cadre mathématique pour traduire les propriétés topologiques de n’importe quel reseau dans un langage mathématique qui permet d’en tirer les propriétés globales du système avec précision et rigueur.
Comme nous l’avons déjà vue plus haut, le même cadre mathématique de la « théorie des graphes » décrit des réseaux physiques totalement différents. Ceux-ci se manifestent dans la manière dont les neurones du tissu cérébral sont connectés, dans les réseaux sociaux, dans les réseaux neuronaux qui sont à la base des algorithmes d’intelligence artificielle, dans l’interconnectivité et interdépendance des réactions biochimiques, etc.
Ce court exposé a mis l’accent sur l’application de cette approche pour injecter la mécanique quantique dans la théorie des graphes chimiques en quantifiant les arêtes liants les atomes d’une molécule donnée suivit par la définition des « matrices de localisation et de délocalisation d’électrons » (LDMs). Dans cette approche, la molécule est conçue comme un réseau d’atomes en interaction où les lignes d’interaction définissant la topologie sont calculées à partir de ce que l’on appelle la « densité d’échange électronique » (Cook et al., 2023). Ces LDMs se sont avérées utiles dans la prédiction des propriétés physicochimiques de plusieurs composés chimiques, y compris, pour décrire l’efficacité des inhibiteurs de corrosion, l’efficacité de répulsion des moustiques des insectifuges ainsi que les propriétés d’absorption de la lumière ultra-violette de la famille de l’acide benzoïque et ses dérivés ainsi que leurs acidités respectives.
Donc, un seul « schème cognitif commun » traverse plusieurs disciplines et applications. En plus, même dans une seule discipline, la chimie quantique computationnelle, dans le cadre de laquelle on définit les matrices de localisation et de délocalisation d’électrons, les applications elles-mêmes traversent plusieurs domaines : de l’industrie (inhibiteurs de corrosion), au contrôle des vecteurs comme les moustiques, à l’enzymologie (biochimie).
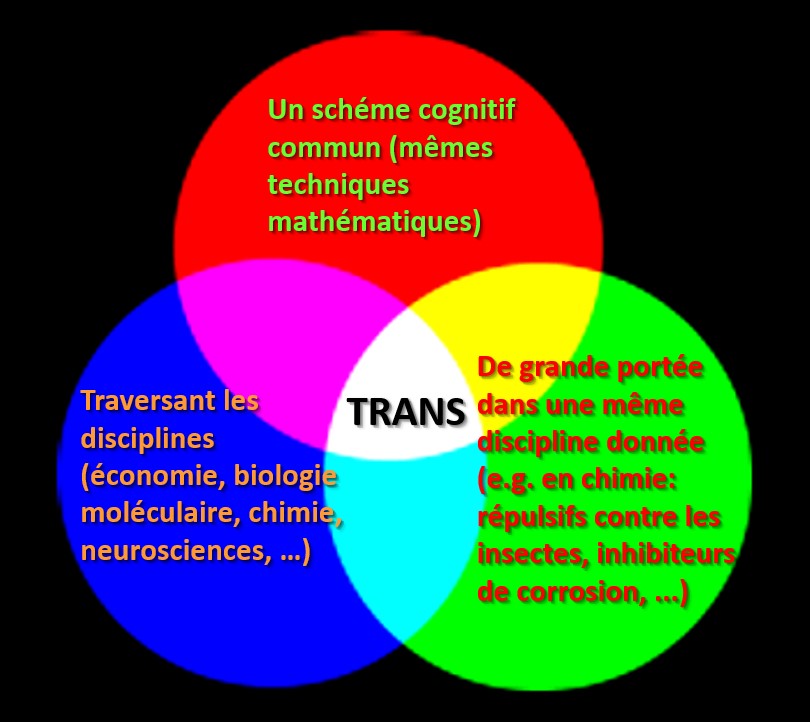
Cette théorie des réseaux est donc le substrat commun de dizaines de domaines d’investigation humaine et d’applications importantes. La Figure 10 illustre ces relations qui satisfont la définition de la transdisciplinarité proposée par Edgar Morin et par Basarab Nicolescu puisque « [c]es différentes entités [plan du métro, tissu cérébral, chaines de réactions chimiques, une molecule …] vivaient dans leur propre monde, régi par ses propres lois, mais elles étaient reliées par des lois cosmiques communes [celles des invariants de la théorie des graphes] engendrant un ordre cosmique commun. »
C’est peut-être une concrétisation, en une certaine mesure, de l’énoncé du grand physicien Richard Feynman : « La nature n’utilise que les fils les plus longs pour tisser ses motifs, de sorte que chaque petit morceau de son tissu révèle l’organisation de toute la tapisserie »[6] (Feynman, 1965).
Figure 10: La transdisciplinarité de l’étude des réseaux par la théorie générale des graphes.
Remerciements
L’auteur remercie le CRSNG, la FCI, Compute Canada et l’Université Mont Saint Vincent pour leur soutien financier.
Bibliographie
Aldous, JM & Wilson RJ (2000) Graphs and Applications: An Introductory Approach, New York, Springer.
Bader RFW (1990), Atoms in Molecules: A Quantum Theory, Oxford U.K., Oxford University Press.
Balaban AT (1976), Chemical Applications of Graph Theory, New York, Academic Press.
Balaban AT (1985), Applications of graph theory in chemistry J. Chem. Inf. Comput. Sci. 25: 334-343.
Balasubramanian K (1994), Integration of graph theory and quantum chemistry for structure-activity relationship, SAR & QSAR Eviron. Res. 2: 59-77.
Bonchev D, Rouvray DH (1991), Chemical Graph Theory: Introduction and Fundamentals, Amsterdam, OPA.
Cook R (2017), Principal components of localization-delocalization matrices: new descriptors for modeling biological activities of organic compounds. Part I: mosquito insecticides and repellents, Struct. Chem, 28: 1527-1538.
Cook R, Ayers PW & Matta CF (2023), Electron Localization-Delocalization Matrices, Berlin, Springer.
Diudea MD, Gutman I & Lorentz J (1999), Molecular Topology, Hauppauge NY, Nova Science Publishers, Inc.
Dmitriev IS (1981), Molecules without Chemical Bonds (English Translation). Moscow: Mir Publishers.
Feynman R (1965), The Character of Physical Law. Massachusetts Institute of Technology, Cambridge, Massachusetts USA, The M.I.T. Press.
Huang TS & Parker RR (1971), Network Theory: An Introductory Course. Massachusetts, Adison-Wesley Publishing Co.
Janezic D, Milicevic A, Nikolic S & Trinajstic N (2007). Graph Theoretical Matrices in Chemistry (Mathematical Chemistry Monographs, Vol. 3). Kragujevac, University of Kragujevac.
Matta CF (2014), Modeling biophysical and biological properties from the characteristics of the molecular electron density, electron localization and delocalization matrices, and the electrostatic potential. J. Comput. Chem, 35: 1165-1198.
Matta CF (2017), De la topographie de la densité électronique ą une théorie quantique des atomes dans les molécules. Le BUP (Physique – Chimie) 111: 825-845.
Matta CF (2018), Molecules as networks: A localization-delocalization matrices approach, Comput. Theor. Chem. 1124: 1-14.
Morin E (1990), Carrefour des sciences, Actes du Colloque du Comité National de la Recherche Scientifique Interdisciplinarité. Paris, Éditions du CNRS.
Nicolescu B (1996), La transdisciplinarité – Manifeste. Paris, Editions du Rocher.
Polanyi M (1967), Life transcending physics and chemistry, Chem. Eng. News (C&EN) 45 (numéro du 21 août): 54-69.
Polanyi M (1968), Life’s Irreducible Structure, Science 160: 1308-1312.
Slepian P (1968), Mathematical Foundations of Network Analysis, New York, Berlin, Heidelberg: Springer-Verlag.
Solé R (2009), Redes Complejas. Barcelona, Tusquets Editores.
Sporns O (2018), Graph theory methods: applications in brain networks, Dialogues Clin Neurosci, 20: 111–121.
Sumar I, Cook R, Ayers PW & Matta CF (2015), AIMLDM: A Program to Generate and Analyze Electron Localization-Delocalization Matrices (LDMs), Comput. Theor. Chem. 1070: 55-67.
Sumar I, Cook R, Ayers PW & Matta CF (2016), Aromaticity of Rings-in-Molecules (RIMs) from Electron Localization-Delocalization Matrices (LDMs), Phys. Script, 91: 013001.
Thom R (1977), Stabilité Structurelle et Morphogénèse, Essai d’une Théorie Générale des Modčles (deuxième édition), Paris, InterEdition.
Toussi CA, Haddadnia J & Matta CF (2020), Drug design by machine-trained elastic networks: Predicting Ser/Thr-protein kinase inhibitors’ activities, Mol. Divers. 25: 899-909.
van Dixhoorn JJ & Evans FJ (1974), Physical Structure in Systems Theory: Network Approaches to Engineering and Economics, London, Academic Press.
von Bertalanffy L (1969), General System Theory: Foundations, Development, Applications. New York, NY, George Braziller, Inc.
Wawer M, Peltason L, Weskamp N, Teckentrup A & Bajorath J (2008), Structure-activity relationship anatomy by network-like similarity graphs and local structure-activity relationship indices, J. Med. Chem. 51: 6075-6084.
[1] « Physics is dumb without the gift of boundary conditions, forming its frame; and this frame is not determined by the laws of physics. »
[2] Ces mots sont soulignés en italique par l’auteur.
[3] « We have seen that physiology interprets the organism as a complex network of mechanisms, and that an organism is like a machine a system under dual control. Its structure is that of a boundary condition harnessing the physical-chemical substances within the organism in the service of physiological functions. »
[4] Ces mots sont soulignés en italique par l’auteur.
[5] Cette section est basée sur le résumé de l’exposé de l’auteur au Centenaire du mathématicien René Thom (1923-2023) présenté le 21 septembre 2023 à l’Institut des Hautes Études Scientifiques (IHS), Bures-sur-Yvette, France [https://indico.math.cnrs.fr/event/9880/timetable/].
[6] « Nature uses only the longest threads to weave her patterns, so that each small piece of her fabric reveals the organization of the entire tapestry ».